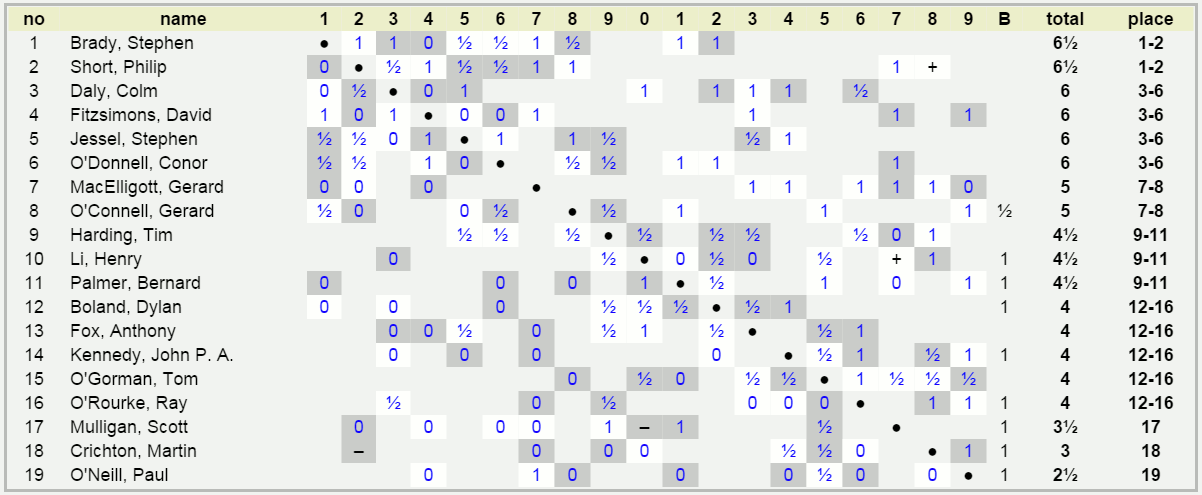
The close finish to this year’s Irish championship brought the possibility of a three-way tie for first place. When two players tie for first, the rule is (as it has been since the 1970s) that the players share the title. But if three or more players finish equal first, tie-breaks are applied to produce a single champion. (The tie-break methods appear to be Median Buchholz, followed by Buchholz, possibly followed by result of individual game.)
Three-way ties are rare (with only the 1996 example involving Richard O’Donovan, Colm Daly, and Tom Clarke), but this year it would only have required Stephen Jessel to win his last round game against Tim Harding, instead of drawing.
In that case Philip Short would have been the winner on tie-break and sole Irish champion. Similarly, with the actual results he was the winner on tie-break of the guaranteed Olympiad place.
But this is puzzling given the crosstable:
Stephen Brady and Philip Short had 6 opponents in common, and they also played each other. This leaves just 2 opponents each that were not in common: Brady played Bernard Palmer and Dylan Boland (both 4½/9 4½/9 and 4/9 respectively), while Short played Scott Mulligan (3½/9) and had a walkover against Martin Crichton (3/9). At first glance, Brady’s opponents did (very slightly) better than Short’s. So how on earth could it happen that Short won the tie-break?
This result seems correct: with these results, and with the current tie-break system, Philip Short is indeed the winner. Why? Answer in a few days.
The reasons include some that appear arbitrary and capricious. Of course this is not and can not be a criticism of Philip Short, who would have been badly treated if on these results the tie-break had gone the other way. But it does raise the question of whether the title of Irish champion should be awarded in this way in three (or more) way ties. The ideal solution would be a playoff at regular time controls; but even accepting that this is difficult to arrange, what exactly is wrong with allowing three players to share the title?